Dropout in Deep Network

在机器学习任务中一提到过拟合，L1和L2正则项绝对是两大利器，但是在深度神经网络中，Hiton老爷子在2014年提出了一种称为Dropout的方法来避免过拟合，方式对比L1和L2更为灵活也是非常高效。

深度神经网络中，在不限制计算的条件下，最佳的正则化方式就是将所有可能组合成的模型进行平均输出，就类似stack的模型融合一样，但是这种方式存在两大问题:

1. 在计算时需要将训练文件进行相应的分离，因为神经网络的训练本身就是需要极多的数据，这么一分离可能会导致数据不够的情况
2. 深度神经网络中的计算量本身就很大，计算多个之后其耗时将会更多

而Dropout却可以完美的解决上述两个缺陷，他的思想很简单:

在训练时对于神经网络的某些神经点击直接进行移除，包括他的入边和出边，而这个移除可以简单的根据一个概率p，这个p一般就是Dropout需要设置的参数

这个参数$p$一般设置为0.5比较好，因为他这样就可能产生$2^n$中网络情况了，极大的增加的参数空间

因此经过Dropout之后两个神经网络的对比如下:

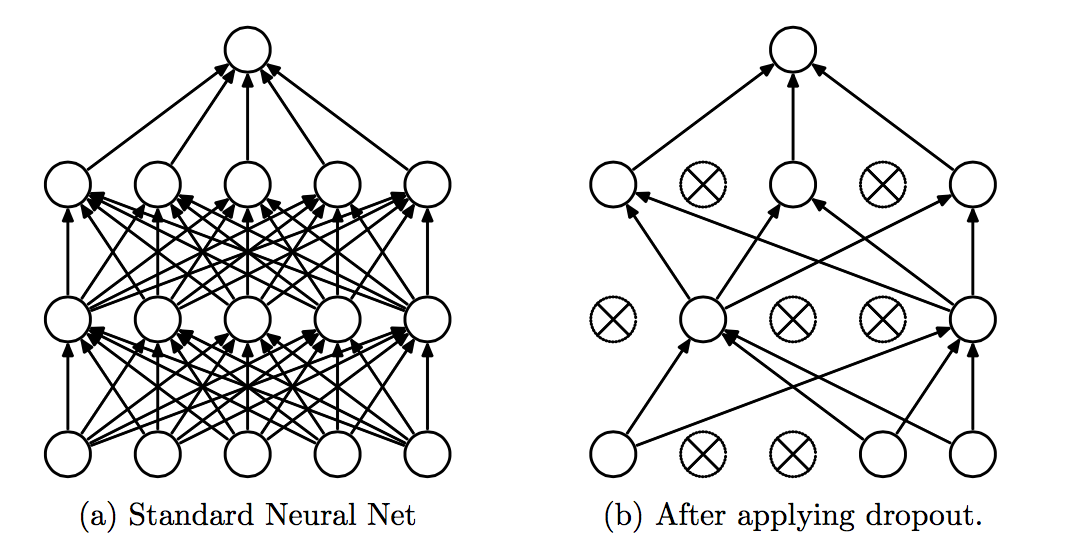
可以看到经过Dropout之后(b)中很多单元节点直接被进行了移除（注意这里是一次min-batch走一次Dropout），使用了Dropout在预测时也是极其的简单:
在预测时这些曾经过移除过的节点仍然正常计划，唯一的差别就是在下一次的权重中乘以概率$p$

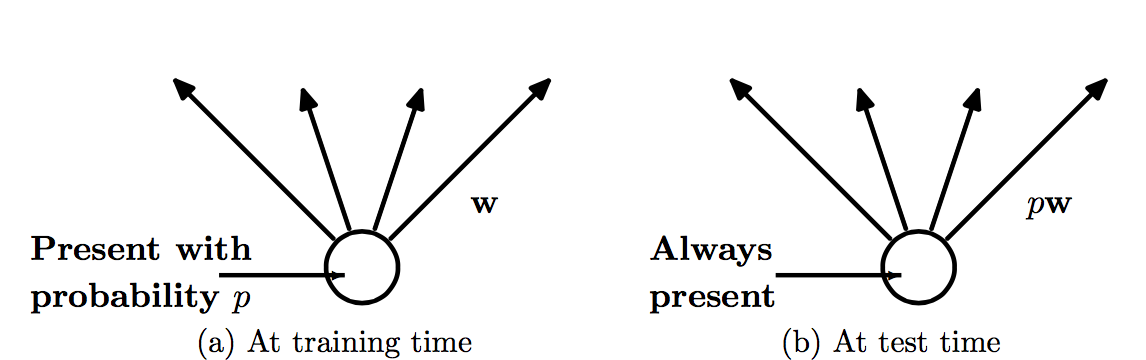
因此针对一个标准深度神经网络,当前层使用$l$来表示，$w$为需要训练的权重,$y$就是各个层的输出，$b$为各个层的偏置，则每一层的标准计算为:
$$z_i^{l+1} = w_i^{l+1}y^l + b_i^{l+1} \\
y_i^{l+1} = f(z_i^{l+1})$$

其中$f$为激活函数

而经过了Dropout之后整个计算过程就会变为这样:
$$r_j^l \sim \text{Bernoulli}(p) \\
\tilde{y}^l = r_j^l y^l \\
z_i^{l+1} = w_i^{l+1}\tilde{y}^l + b_i^{l+1} \\
y_i^{l+1} = f(z_i^{l+1})$$

也就是下图的样纸:

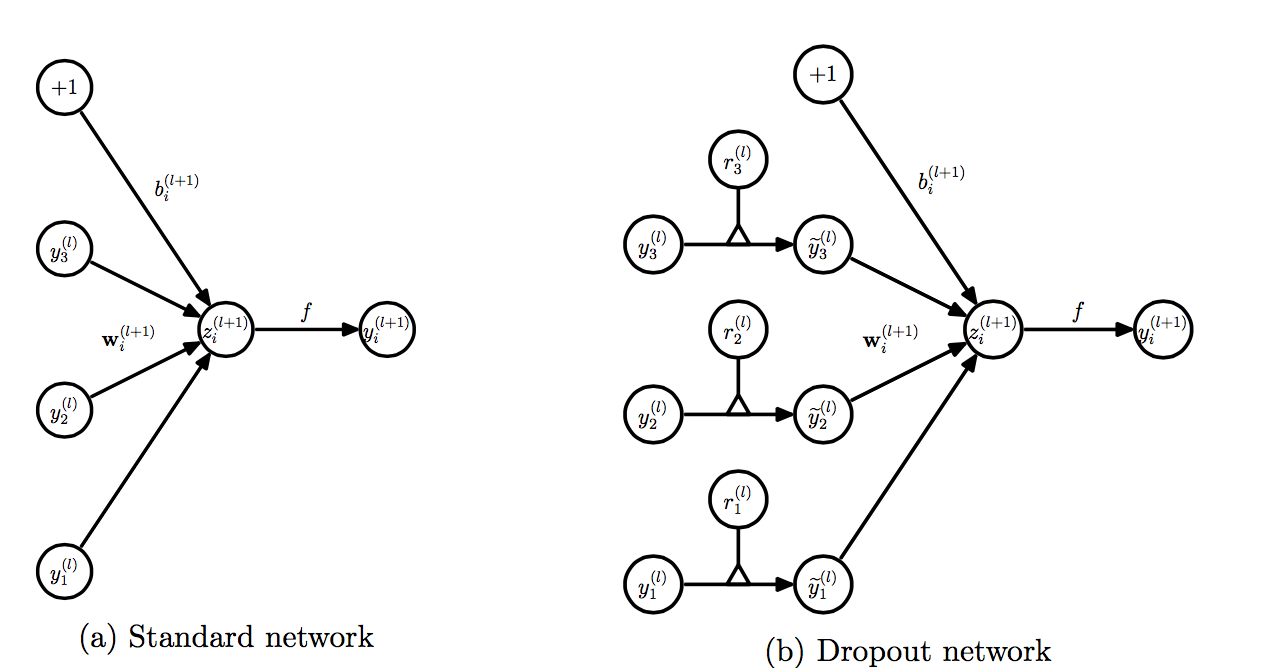
而在预测的时候，只需要在Dropout层输出的权重上乘$p$即可:$w_{test}^l = pw^l$

关于使用了Dropout之后，如果使用SGD进行优化的话其梯度仍旧可以按照来的方式计算，不过他是在一次min-batch来计算一次Dropout

也就在同一次min-batch中，Dropout层中的点击移除与否的分布是一样的，不同的Dropout中是可能不一样的

文献的实验正常传统的深度神经网络中加入了Dropout之后在训练集上面的误差可能会增大，但是在测试集上其误差会变小，也就是降低的过拟合的程度

Dropout in Recurrent Network

虽然Dropout中在传统的深度网络中很好使，但是直接用于RNN这类递归型的神经网络却不是很好使，原因是如果直接将Dropout层防止在Memory Cell中,循环会放大噪声，扰乱它自己的学习。
Wojciech Zaremba针对此问题提出的核心解决方法就是在输入和输出层加Dropout:
$$\begin{pmatrix}
i\\
f\\
o\\
g
\end{pmatrix}
=
\begin{pmatrix}
sigm\\
sigm\\
sigm\\
tanh
\end{pmatrix}
T_{2n,4n}
\begin{pmatrix}
D(x_t)\\
h_{t-1}^l
\end{pmatrix}
$$

上面是一个LSTM的式子，计算三个门单元以及当前信息单元，$D$就是Dropout层,这里是加在了输入层

文献

1. Srivastava, Nitish, et al. “Dropout: A simple way to prevent neural networks from overfitting.” The Journal of Machine Learning Research 15.1 (2014): 1929-1958.
2. Zaremba, Wojciech, Ilya Sutskever, and Oriol Vinyals. “Recurrent neural network regularization.” arXiv preprint arXiv:1409.2329 (2014).

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。